NCERT Solutions For Class 5 Maths Chapter 6 Be My Multiple, I’ll Be Your Factor -

NCERT Solutions for Class 5 Maths Chapter 6 Be My Multiple, I’ll be Your Factor has been published by exammodalpaper. You can now download the Class 5 Maths Ch 6 Questions and Answers PDF here. This NCERT Solutions for Class 5 Maths contains answers of all questions asked in Chapter 6 in textbook. Therefore you can prerefer it to solve Be My Multiple, I’ll be Your Factor exercise questions and learn more about the topic.In lesson 6 of Class 5 Maths, students learn to jump 2 or 3 numbers and use them to form a series. It involves finding numbers that can be divided by 2, 3, and 4. They will learn about multiples of a number in sequence, as well as least common factors and other similar concepts.

These materials are prepared as per the CBSE and ncert syllabus (2023-2024) formulated for Class 5. Maths is an important subject, and it is always crucial to have a thorough understanding of the basics. These elementary concepts form the base for higher education and also shape future opportunities. The solved questions provided here follow the Class 5 NCERT Textbook curriculum.

NCERT Solutions Class 5 Maths Chapter 6 specifically deals with concepts such as multiples and factors. These concepts are explained in a way that makes it easier for students to understand and comprehend the topic. For instance, there are direct questions and application questions. All questions are answered with step-by-step explanations for students to understand easily. Furthermore, these selected questions are the most probable and highly anticipated in the annual exam.

Table of Contents

NCERT Solutions Class 5 Maths Chapter 6 Be My Multiple, I’ll Be Your Factor

1. The hungry cat is trying to catch Kunjan, the mouse. Kunjan is now on the 14th step, and it can jump 2 steps at a time. The cat is on the third step. She can jump 3 steps at a time. If the mouse reaches 28, it can hide in the hole. Find out whether the mouse can get away safely.

a) The steps on which the mouse jumps

Solution:- The steps on which the mouse jumps are 16, 18, 20, 22, 24, 26 and 28.

b) The steps on which the cat jumps

Solution:- The cat jumps from the 3^rd step to the 6, 9, 12, 15, 18, 21, 24, and 27^th steps.

c) The steps on which both the cat and the mouse jump

Solution:- The steps on which both the cat and the mouse jump are the 18^th and 24^th steps.

d) Can the mouse get away?

Solution:- Yes, the mouse can get away.

2. Find out

If the cat starts from the 5^th step and jumps five steps at a time, and the mouse starts from the 8^th step and jumps four steps at a time, can the mouse get away?

Solution:- In this case

(a) The steps on which the mouse jumps are 8, 12, 16, 20, 24 and 28

(b) The steps on which the cat jumps are 5, 10, 15, 20 and 25.

(c) The step on which both of the cat and mouse jump is 20.

(d) Since their 4th jump is on step 20 together so the mouse will not get away safely.

3. Who is Monto waiting for?

Monto cat is waiting for somebody. Do you know for whom he is waiting?

There is a trick to find out.

Mark with a red dot all the numbers which can be divided by 2.

Mark a yellow dot on the numbers which can be divided by 3 and a blue dot on the numbers which can be divided by 4.

Solution:-

(i) Which are the boxes that have dots of all three colours?

Solution:- The boxes with dots of all three colours are 12, 24, 36, 48, and 60.

(ii) What are the letters on top of these boxes?

Solution:- The letters on top of these boxes are M, O, U, S, and E.

(iii) Write the letters, M, O, U, S, and E, in order.

Solution:- MOUSE,

So, Monto cat is waiting for Mouse.

4. Meow Game: To play this game, everyone stands in a circle. One player calls out ‘one’. The next player says ‘two’ and so on. A player who has to call out 3 or a number which can be divided by 3 has to say ‘Meow’ instead of the number. One who forgets to say ‘Meow’ is out of the game. The last player left is the winner.

Which numbers did you replace with ‘Meow’?

Solution:-

The numbers which replace with ‘Meow’ and multiples of 3 are,

3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45 and so on.

5. We say these numbers are multiples of 4. Find the numbers.

Play the game by changing the number to 4. Now, which numbers did you replace with ‘Meow’? These numbers are the multiples of 4.

Solution:-

The numbers which replace with ‘Meow’ and multiples of 4 are,

4, 8, 12, 16, 20, 24, 28, 32, 36, 40, and so on.

(i) Write any ten multiples of 5.

Solution:-

Ten multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, and 50.

6. Common Multiples

(i) Think of a number. If it is a multiple of 3, write it in the red circle. If it is a multiple of 5, write it in the blue circle.

Solution:-

6 and 36 are multiple of 3.

10 and 40 are multiple of 5.

Then,

(ii) Some numbers are multiples of both 3 and 5. So we can say that they are both 3 and 5. Think! If you write the multiples common to 3 and 5 in the purple part, then will they still be in both the red and the blue circles?

Solution:-

15 and 30 are the numbers which are multiples of both 3 and 5.

7. Repeat the game by putting the multiples of 4, 6 and 5 in the circles.

Solution:-

(i) What common multiples of 5 and 6 did you write in the green part?

Solution:- 30 and 60

(ii) What common multiples of 4 and 6 are written in the orange part?

Solution:- 12 and 24

(iii) In which coloured part did you write the common multiples of 4, 6 and 5?

Solution:- They are written in the grey part.

(iv) What is the smallest common multiple of 4, 6 and 5?

Solution:- 60

8. Tamarind seeds.

(i) Sunita took some tamarind (imli) seeds. She made groups of five with them and found that one seed was left over. She tried making groups of six and groups of four. Each time one seed was left over. What is the smallest number of seeds that Sunita had?

Solution:- In the previous question we have seen that the smallest common multiple of 4, 5 and 6 is 60.
Hence, the smallest number of seeds which Sunita has is 60 +1 = 61

9. More tamarind seeds

Ammini arranges 12 tamarind seeds in the form of different rectangles. Try to make more rectangles like this using 12 tamarind seeds. How many different rectangles can you make?

Solution:- I got four different rectangles, as shown in the figure below,

(i) If there are 15 tamarind seeds, how many rectangles can you make?

Solution:-

10. Colouring the Grid

In the grid here, a rectangle made of 20 boxes is drawn.

The width of this rectangle is 2 boxes.

(i) What is its length?

Solution:- The length is 10 boxes.

(ii) Colour a rectangle made of 20 boxes in some other way.

Solution:-

(iii) What is the length and width of the rectangle you coloured?

Solution:-Rectangles of following length and width can be made: 5 x 4 , 20 x 1

(iv) In how many ways can you colour a rectangle of 20 boxes? Colour them all in the grid, and write the length and width of each rectangle you have coloured.

Solution:-

The length and width of rectangle 1 are 5 and 4, respectively.

The length and width of rectangle 2 are 4 and 5, respectively.

The length and width of rectangle 3 are 20 and 1, respectively.

11. There are 18 bangles on the rod. Meena is trying to group them. She can put them in groups of 2, 3, 6, 9 and 18 without any bangle being left.

(i) How many groups will she have if she makes groups of 1 bangle each?

Solution:- 18 groups of 1 bangle each.

(ii)Now complete the table, for different numbers of bangles. For each number see what different groups can be made.
Ans.

12. Fill the chart

1.Complete the multiplication chart given here:
Ans.

Look at the green boxes in the chart. These show how we can get 1£ by multiplying different numbers.
12 = 4 x 3, so 12 is a multiple of both 3 and 4.12 is also a multiple of-6 and 2, as well as 12 and 1. We pay 1, 2, 3, 4, 6, and 12 are factors of 12.

(i) What are the factors of 10? Can you do this from the chart?

Solution:- The factors of 10 are: 1, 2, 5,10 Yes, we can find it from the chart also.

(ii) What are the factors of 36?

Solution:- The factors of 36 are: 1, 2, 3, 4, 6, 9,12,18 and 36.

(iii) Find out all the factors of 36 from the multiplication chart.

Solution:- From the multiplication chart, the factors of 36 are 1, 2, 3, 4, 6, and 9.

(iv) What is the biggest number for which you can find the factors from this chart?

Solution:- The biggest number for which can find factor from the chart is 144.

(v) What can you do for numbers bigger than that?

Solution:- First, we will extend the multiplication chart and then complete the chart.

Common Factors
1.Write the factors of 25 in the red circle and the factors of 35 in the blue circle.
Ans.

2.Which are the factors you have written in the common part of both circles? These are common factors of 25 and 35.
Ans. 1 and 5.

3.Now write the factors of 40 in the red circle and 60 in the blue circle.
Ans.

4.What are the factors written in the common part of the circle? Which is the biggest common factor of 40 and 60?
Ans. The factors written in common part of the circle are;1, 2, 4, 5,10 and 20
The biggest common factor of 40 and 60 is 20.

Factor Tree
1.Look at the factor tree. Now you can make another tree like this?

Ans.

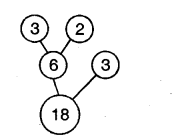
2.In how many ways can you draw a factor tree for 24? Draw three of them below.
Ans.

3.Try drawing the factor tree using other numbers also.
Ans. 36 can be factorized as given factor trees.

48 can be factorized as given factor trees.

Tiling Problems
1.There is a garden in Anu’s house. In the middle of the garden there is a path. They decided to tile the path using tiles of length 2 feet, 3 feet and 5 feet.
The mason tiled the first row with 2 feet tiles, the second row with 3 feet tiles and the third row with 5 feet tiles. The mason has not cut any of the tiles. Then what is the shortest length of the path?

Ans. The smallest common multiple of 2, 3 and 5 is the shortest length of the path.
Multiples of 2: 2, 4, 6, 8, 10,12,14, 16,17, 18, 20, 22, 24, 26, 28, 30
Multiples of 3: 3, 6, 9,12, 15, 18, 21, 24, 27, 30
Multiples of 5: 5, 10, 15, 20, 25, 30
The smallest common multiple is 30.
Hence, the answer is 30 feet.

2. Manoj had made a new house. He wants to lay tiles on the floor. The size of the room is 9 feet x 12 feet. In the market, there are three kinds of square tiles: 1 foot x 1 foot, 2 feet x 2 feet and 3 feet x 3 feet. Which size of tile should he buy for his room, so that he can lay it without cutting?
Ans. 2 is not a factor of 9 feet which is the width of the room.
1 and 3 are factors of both 9 and 12.
Hence, Manoj can buy tiles of 1 foot x 1 foot or 3 feet x 3 feet.
These tiles can be laid without cutting.

3. Rani, Geetha and Naseema live near each other. The distance from their houses to the road is 90 feet. They decided to tile the path to the road. They all bought tiles of different designs and length. Rani bought the shortest tile, Geetha bought the middle sized one and Naseema bought the longest one. If they could tile the path without cutting any of the tiles, what is the size of the tiles each has bought? Suggest 3 different solutions. Explain how you get this answer.
Ans. 90 can be factorized as follows:
90 = 1 x 90
90 = 2 x 45
90 = 3 x 30
90 = 5 x 18
90 = 6 x 15
90 = 9 x 10
Hence possible tiles can be as follows: 1 x 1, 2 x 2, 3 x 3, 5 x 5, 6 x 6, etc.

NCERT Solutions for class 5 Maths Chapter 6 Be My Multiple, I’ll be Your Factor

NCERT Solutions Class 5 Maths Chapter 6 Be My Multiple, I’ll Be Your Factor

Related Post :-

Frequently Asked Questions

Leave a comment Cancel reply