NCERT Solutions for Class 5 Maths Chapter 3 How Many Squares?
Here we have given ncert solutions for class 5 maths chapter 3 How Many Squares?.NCERT Solutions for Class 5 Maths Chapter 3 How Many Squares? are part of NCERT Solutions for Class 5 Maths.How Many Squares helps students to draw squares from a given set of dots. With questions related to measuring sides of squares, this chapter contains a series of questions which will help them improve their competence on the subject.
In Class 5 Maths, Chapter 3 titled “How Many Squares?”, students are introduced to the world of geometry. This chapter focuses on squares and helps students understand their properties. The main objective is to develop a strong foundation in geometry by teaching students about the characteristics of squares and the relationship between their sides and angles. To assist students in their learning process, ncert solutions for class 5 maths chapter 3. These solutions serve as a helpful guide, offering step-by-step explanations and solutions to the exercises. By using these solutions, students can enhance their problem-solving skills and improve their understanding of geometry.
Get Solutions for NCERT Class 5 Maths Chapter 3 How Many Squares
1.
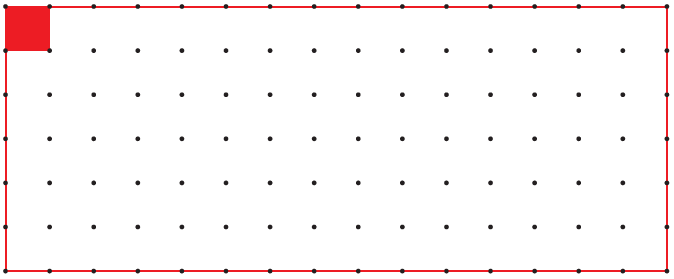
(i) Measure the side of the square on dotted sheet. Draw here as many rectangles as possible using 12 such squares.
Ans.The side of the square is 1 centimetre.
Following figure shows the possible rectangles using 12 such squares.
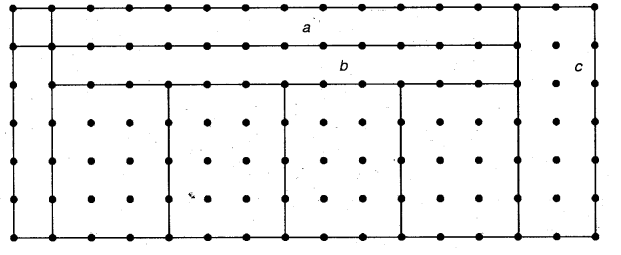 • How many rectangles could you make?
• How many rectangles could you make?
Solution:-We can make 7 rectangle.
2. Each rectangle is made out of 12 equal squares, so all have the same area, but the length of the boundary will be different.
Solution:-
From the above figure, we can say that rectangles 1 and 2 have the longest perimeter.
We know that, perimeter of rectangle = 2 (length + breadth)
= 2 (1 + 12)
= 2 × 13
= 26 cm
(i) Which of these rectangles has the longest perimeter?
Solution:-
From the above figure we can say that, rectangle 3, rectangle 4, rectangle 5 and 6 rectangle has the smallest perimeter.
We know that, perimeter of rectangle= 2 (length + breadth)
= 2 (3 + 5)
= 2 × 8
= 16 cm
3.Which of these rectangles has the smallest perimeter?
Ans. The rectangle measuring 3 x 4 cm has the smallest perimeter.
3.
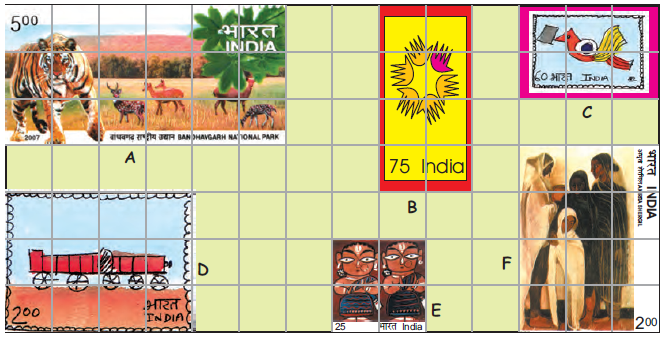
Look at these interesting stamps.
(a) How many squares of one centimetre side does stamp A cover? ________
And stamp B? ________
Ans. Area = length x breadth
= 6 x 3 = 18 square cm
•And stamp B?
Ans. Area = length x breadth
= 4 x 2 = 8 square cm
(b)Which stamp has the biggest area?
Ans. Stamp A has the biggest area.
•How many squares of side 1 cm does this stamp cover?
Ans. This stamp covers 18 squares of side 1 cm.
•How much is the area of the biggest stamp?
Ans. 18 square cm.
(c)Which two stamps have the same area?
Ans. Stamp D and F have the same area.
•How much is the area of each of these stamps?
Ans. The area of stamp D and F each is 12 square cm.
(d)The area of the smallest stamp is —— square cm.
Ans.The area of smallest stamp ‘E’ = length × breadth
= 2 × 2
= 4 cm2
Therefore, the area of the smallest stamp is 4 square cm.
(i) The difference between the area of the smallest and the biggest stamp is _____ square cm.
Solution:-
Area of the biggest stamp = 18 cm2
Area of the smallest stamp = 4 cm2
Then,
The difference between the area of the smallest and the biggest stamp = 18 – 4
= 14 cm2
Guess
(a)Which has the bigger area-one of your footprints or the page of this book?
Ans.The area of page of this book. .
(b)Which has the smaller area-two five-rupee notes together or a hundred rupee note?
Ans.A hundred rupee note.
(c)Look at a 10 rupee note. Is its area more than hundred square cm?
Ans.No, the area of 10 rupee note is less than 100 square centimetre.
(d)Is the area of the blue shape more than the area of the yellow shape? Why?
Ans.No, the area of blue shape is equal to the area of yellow shape. This can be easily proved by taking a cutout of these shapes and by calculating their areas using the square grid paper.
(e)Is the perimeter of the yellow shape more than the perimeter of the blue shape? Why?
Ans.No, the perimeter of yellow shape is less than the perimeter of the blue shape. This can be proved by measuring their boundaries by ruler or by thread.
5. Write the area (in square cm) of the shapes below.
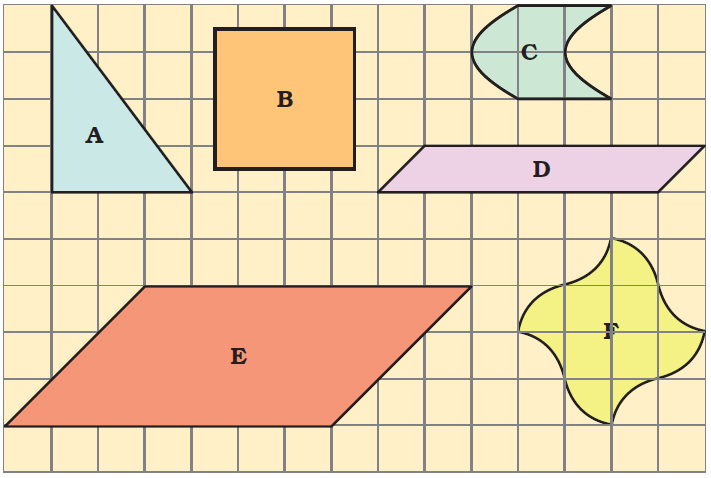
Ans.Area of triangle A = Half of area of rectangle
= 1/2 x 12 = 6 square cm.
Area of square B = 4 complete squares + 8 half squares + 4 quarter squares
= 4 + 1/2 x8 + 1/4 x 4
= 4 + 4 + l = 9 square cm
Area of shape C = 2 + 1/2 x 0 + 2
= 2 + 2 = 4 square cm
Area of shape D = 5 + 1/2 x 2 + 0
= 5 + 1 = 6 square cm
Area of shape E = 18 + 1/2 x 6 + 0
= 18 + 3 = 21 square cm
Area of shape F = 4 + 1/2 x 0 + 4
= 4 + 4 = 8 square cm.
6. The blue triangle is half of the big rectangle. The area of the big rectangle is 20 square cm. So the area of the blue triangle is _______ square cm.
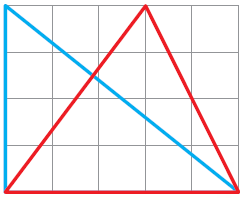
Solution:-
From the question,
Area of the big rectangle is 20cm2.
Area of the blue triangle is half of the big rectangle = 20/2
= 10 cm2
7. In the figure below, there are two halves of two different rectangles.
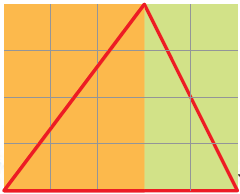
Find the area of the two rectangles in the figure. What is the area of the red triangle? Explain.
From the figure, we can say that,
The orange rectangle contains 12 squares
So, the area of the orange rectangle = 12 cm2
Then, the green rectangle contains 8 squares
So, the area of the green rectangle = 8 cm2
Now, the area of the orange portion of the triangle = 12/2 = 6 cm2
The area of the yellow portion of the triangle = 8/2 = 4 cm2
Therefore, the area of the red triangle = 6 + 4
= 10 cm2
8. Suruchi drew two sides of a shape. She asked Asif to complete the shape with two more sides so that its area was 10 square cm.
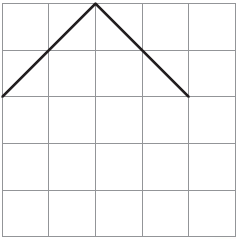
He completed the shape like the following:
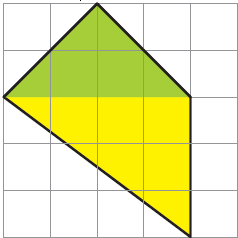
(i) Is he correct?
Solution:- Yes, he is correct.
(ii) Explain how the green area is 4 square cm and the yellow area is 6 square cm.
Solution:-
Green area contains = 2 complete square + 4 half square
= 2 + (½ × 4)
= 2 + 2
= 4 cm2
Yellow area contains = 3 complete square + 2 more than half + 2 half filled
= 3 + 2 + (½ × 2)
= 3 + 2 + 1
= 6 cm2
Practice Questions
1. This is one of the sides of a shape. Complete the shape so that its area is 4 square cm.
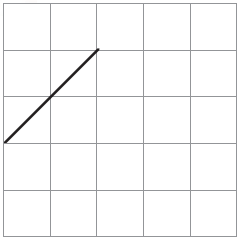
Solution:-
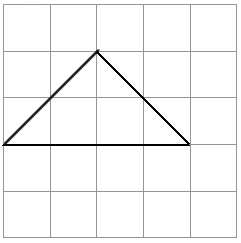
The completed shape = 2 complete square + 4 half square
= 2 + (½ × 4)
= 2 + 2
= 4 cm2
2. Two sides of a shape are drawn here. Complete the shape by drawing two more sides so that its area is less than 2 square cm.
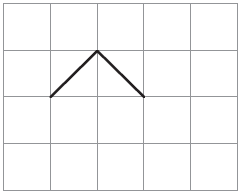
Solution:-
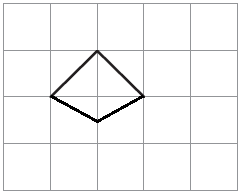
3. Here is a rectangle with an area of 20 square cm.
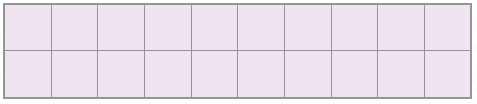
a) Draw one straight line in this rectangle to divide it into two equal triangles. What is the area of each of the triangles?
Solution:-
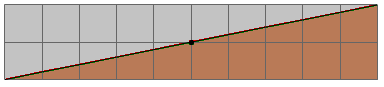
Area of rectangle = 10 × 2
= 20 cm2
Then, area of two equal triangles = 20/2
= 10 cm2
Because, it is given that straight line divides rectangle in to two equal triangles.
b) Draw one straight line in this rectangle to divide it into two equal rectangles. What is the area of each of the smaller rectangles?
Solution:-

Area of big rectangle = 10 cm2
The area of each of the smaller rectangle = 20/2
= 10 cm2
(i) What is the area of the rectangle?
Solution:- Area of rectangle = length × breadth
= 2 × 5
= 10 cm2
(ii) What is the area of each of the triangles?
Solution:- Area of each triangle = ½ × area of the smaller rectangle
= ½ × 10
= 5 cm2
4. Puzzle with five squares
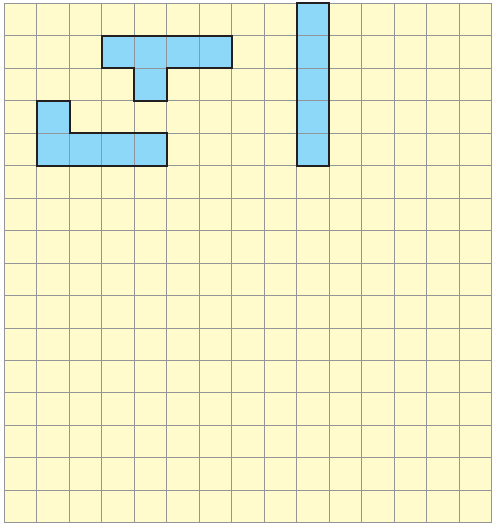
(a)How many different shapes can you draw?
Ans. 12 different shapes can be drawn using 5 such squares.
(b)Which shape has the longest perimeter? How much?———cm
Ans. The perimeter of all shapes (except fig no. 3) is 12 cm.
(c)Which shape has the shortest perimeter? How much?——–cm
Ans. The perimeter of shape 3 is the shortest.
(d)What is the area of the shapes?——— square cm. That’s simple!
Ans. Area of each shape is 5 square cm, because each of them is made of 5 similar squares.
5. Ziri tried to make some tiles. She started with a square of 2 cm side and made shapes like the following:
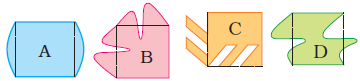
Look at them carefully and find out:
(i) Which of these shapes will tile a floor (without any gaps)?
Solution:-
By observing the given figure, shape C and shape D will tile a floor without any gaps.
Related Post :-
Chapter 4. Parts and Wholes
Chapter 5. Does it Look the Same?
Chapter 6. Be My Multiple, I’ll be Your Factor
Chapter 7. Can You See the Pattern?
Chapter 8. Mapping Your Way
Chapter 9. Boxes and Sketches
Chapter 10. Tenths and Hundredths
Chapter 11. Area and its Boundary
Chapter 12. Smart Charts
Chapter 13. Ways to Multiply and Divide
Chapter 14. How Big? How Heavy?
NCERT Solutions Class 5 to 10
- NCERT Solutions for class 5 Maths
- NCERT Solutions for class 5 EVS
- NCERT Solutions for class 5 Paryayana Adyayan
- NCERT Solutions for class 5 English
- NCERT Solutions for class 5 Hindi
Frequently Asked Questions on NCERT Solutions for Class 5 Maths Chapter 3
Q1. What is Chapter 3 of Class 5 Maths NCERT textbook about? Chapter 3 of Class 5 Maths NCERT textbook is titled “How Many Squares?” This chapter introduces students to the concept of squares and focuses on developing their understanding of squares and their properties.
Q2. What topics are covered in Chapter 3? Chapter 3 covers various topics related to squares, such as identifying and understanding the properties of squares, exploring the relationship between sides and angles of squares, and counting the number of squares in a given figure.
Q3. Why are NCERT solutions important for Class 5 Maths Chapter 3? NCERT solutions for Class 5 Maths Chapter 3 provide step-by-step explanations and solutions to the exercises given in the textbook. These solutions help students to understand the concepts better and enhance their problem-solving skills.
Q4. How can NCERT solutions assist students in learning about squares? NCERT solutions provide clear explanations and examples that aid students in understanding the properties of squares. They also guide students on how to count squares in different figures. By using these solutions, students can strengthen their grasp of the topic and improve their performance in examinations.
Q5. Are NCERT solutions for Class 5 Maths Chapter 3 easy to understand? Yes, NCERT solutions for Class 5 Maths Chapter 3 are designed to be student-friendly and easy to understand. They are prepared by subject matter experts who ensure that the solutions are presented in a simplified manner, making it easier for students to comprehend and apply the concepts.
Q6. How can I access the NCERT solutions for Class 5 Maths Chapter 3? The NCERT solutions for Class 5 Maths Chapter 3 can be accessed from various sources. They are available in the official NCERT website, in the Class 5 Maths textbook, and also in online educational platforms that provide study materials and resources for students.
Q7. Can NCERT solutions be helpful for exam preparation? Yes, NCERT solutions are highly beneficial for exam preparation. They provide a thorough understanding of the concepts covered in the chapter and offer practice exercises that are similar to those that might appear in exams. By solving these exercises using the NCERT solutions, students can gain confidence and improve their performance in exams.
Q8. Can parents and teachers also use NCERT solutions for Class 5 Maths Chapter 3? Absolutely! NCERT solutions are not only helpful for students but also for parents and teachers. Parents can use these solutions to assist their children with homework and provide additional support in understanding the concepts. Teachers can incorporate these solutions into their lesson plans to supplement classroom teachings and assess students’ understanding of the chapter.
Q9. Are the NCERT solutions for Class 5 Maths Chapter 3 accurate? Yes, the NCERT solutions for Class 5 Maths Chapter 3 are prepared by subject matter experts and are accurate. They are in line with the NCERT curriculum and provide reliable solutions to the exercises given in the textbook.
Q10. Can I rely solely on NCERT solutions for exam preparation? While NCERT solutions are an excellent resource, it is recommended to supplement your exam preparation with additional study materials, practice questions, and reference books. This will provide a comprehensive understanding of the subject and help you perform well in exams.
Share to help